..

业务报警智能降噪的那些事

近半年工作，一大部分时间在探索监控报警的智能降噪。用这篇博客整理个人点点滴滴的思考，希望可以不断的持续更新..

背景介绍

监控的重要性不言而喻，它就相当于 SRE 的眼睛。但由于监控系统静态规则的局限性，经常会产生一些误报，e.g. 促销冲高回落(尖刺)，小流量波动, 季节性趋势下跌，入口下跌等等。轻则形成针对人的「DDOS攻击」，重则导致真正的故障被忽略(狼来了的故事)。所以如何利用算法自动识别噪音，已成为当务之急，将会大大降低人肉处理报警的成本，为公司节省成本。

准确率量化

个人认为算法的效果量化是最为关键的一步，故提到最开头。就像优化程序的性能一样，不做 profile，像个无头苍蝇一样去尝试，肯定是无疾而返。而效果的量化又分为 人工标记 + 回归测试:

1) 人工标记

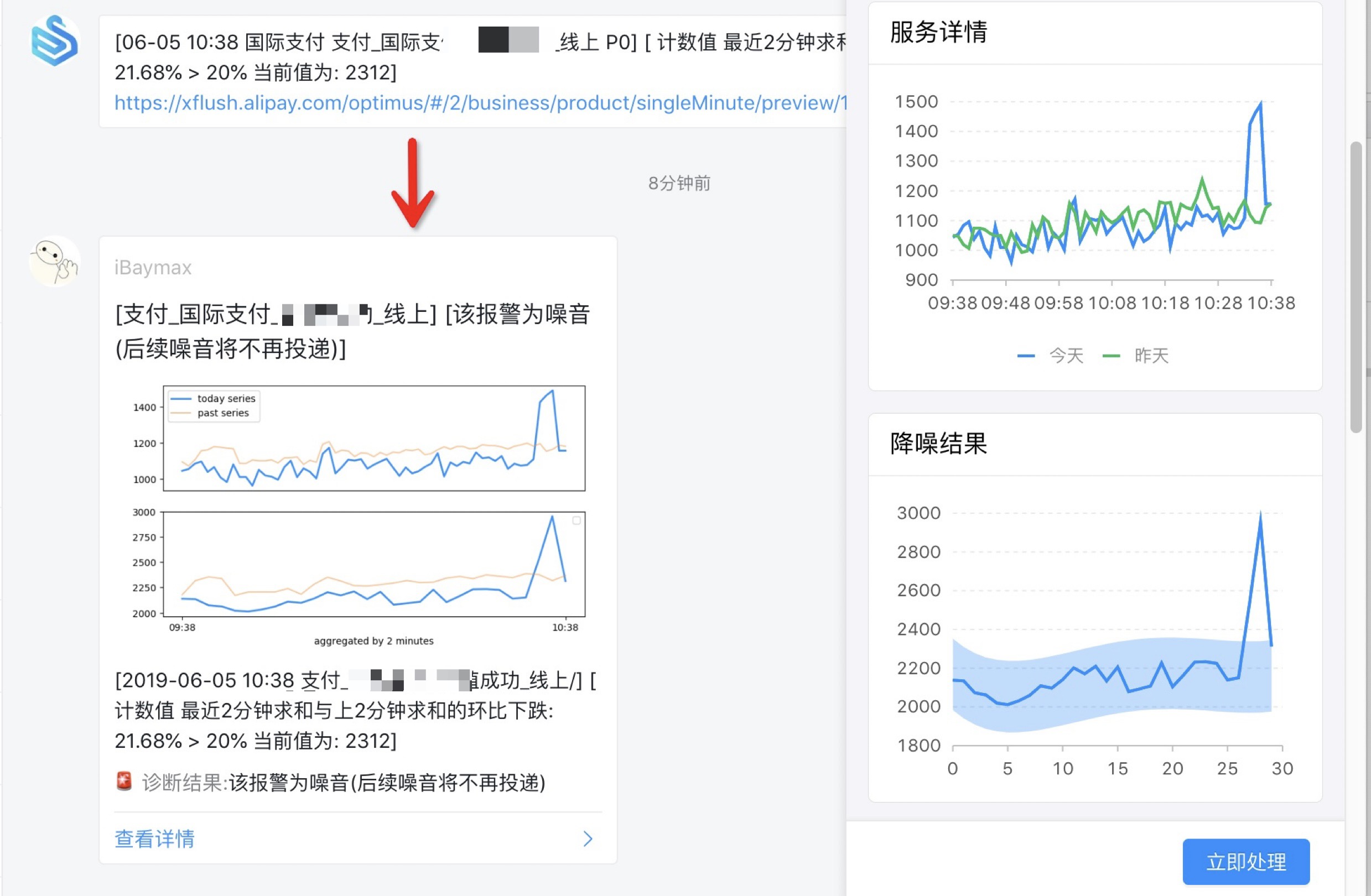
在报警详情页中，界面底部会有一个「立即处理」的按钮，点击后处理的页面就会像支付宝收银台一样咻的一下弹出来，供人工标记噪音还是异常。同时提供 at 花名转发报警 和 关闭报警一段时间的功能。

2) 回归测试

当标记的数据正负样本不平衡的情况下，准确率这个评价指标有一定的缺陷。举个极端的例子: 若标记的数据样本中95个为噪音，5个为异常，算法直接判断所有报警为噪音，最后的准确率为95%。但现实是当一个异常真的发生时，报警被误杀是完全无法接受的。

所以想到引入之前上学时老师计算平时分&期末考试成绩时，使用的 Precision，Recall 和 F-Score 的概念，也就是说我们对 Recall 的要求是非常高的，情愿发出100次警报，把其中5次异常都预测正确了，也不要只识别正确其他95次噪音。

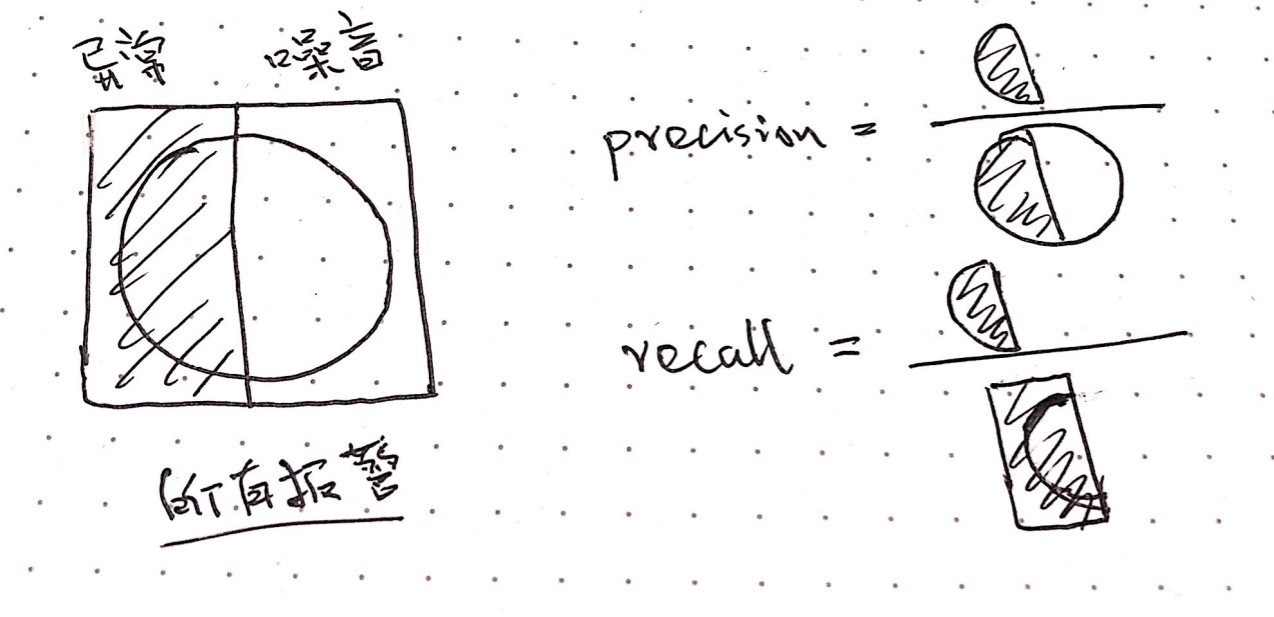
这个地方还挺绕但也挺有趣的，可以直接看我画的图(上方的 「异常」和「噪音」代表 groundtruth，圆圈表示 prediction，然后 precision 和 recall 衡量的是异常检测的效果)： UNADJUSTEDNONRAW_thumb_5d09

举个栗子: 目标: 衡量异常检测的指标 标记样本: 90个为噪音，10个为异常. 算法结果: 5个为异常(判断正确, i.e. TP)，95个为噪音

Positive / Negative: 预测的结果 True / False: 是否预测正确

# 1. 准确率:
accuracy = (TP + TN) / TOTAL = (5 + 90) / 100 = 95%
# 2. F Score:
precision = TP / (TP + FN) = 5 / 5 = 100%
recall = TP / (TP + FP) = 5 / 10 = 50%
f1 = 2 / (1/precision + 1/recall) = 2 * 100% * 50% / (100% + 50%) = 66%

告警整体流程

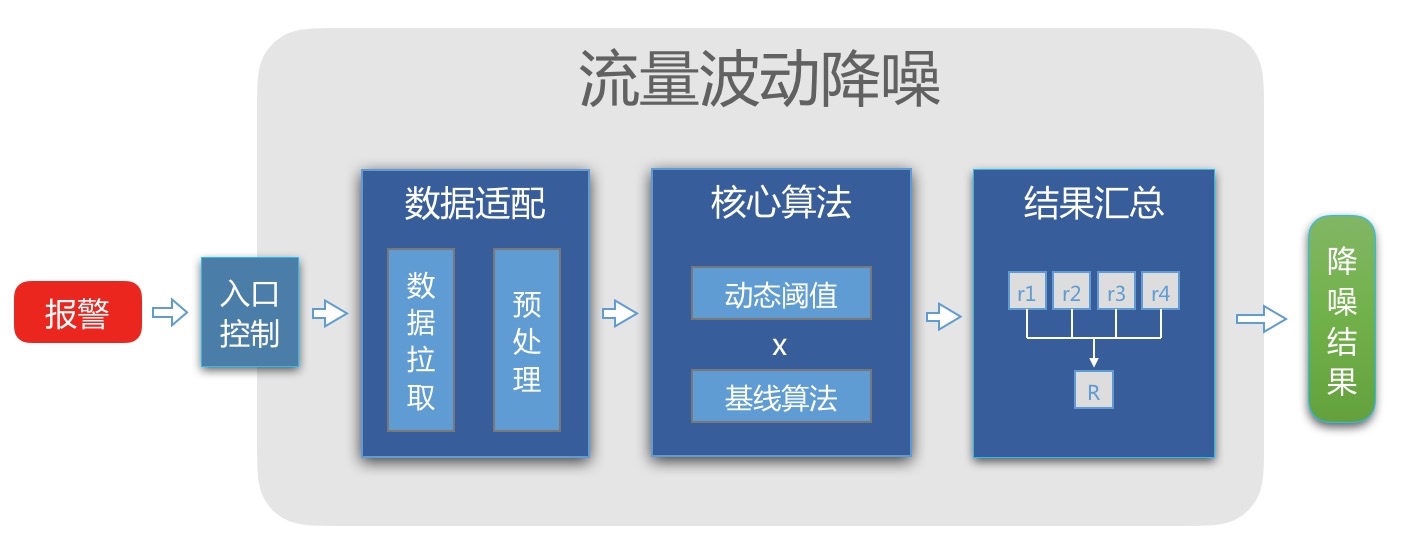
1. 入口控制

对自定义预警做了准入的限制，例如：

  1. 只处理监控类型为"请求量"与"成功量"的报警.
  2. 只处理产品插件为"分钟统计/多Key", “分钟统计/无Key”, “常用服务指标"的报警.
  3. 降噪黑名单, e.g. 代扣撤销.
  4. …

2.1 拉取监控数据

拉取 N x 30 分钟 x 8天 的监控数据。

N 的定义: 监控中配置的环比时间, e.g. 如果配置的为“最近10分钟与上10分钟的环比”, N 就等于 10. 因为某些监控业务量过小(tpm < 10)，所以波动很大，所以在配置监控时就会设置 N 分钟的聚合，tradeoff 是在牺牲报警实效性的情况下，获取更加平滑的数据。

一开始是自己写了一个聚合的函数，后来发现 pandas 有对应很优雅的函数(resample)，分享一下:

# 按时间聚合:
df = df.set_index('ds')
df = df.resample('30T'，level=0，label='right'，closed='right').sum()

2.2 拉取监控数据

Normalization: 对上一步拉取的每天数据按N分钟聚合, 最后输入都是 30分钟 * 8天 的二维矩阵。 **去除离群点：**根据故障时间段或正态分布的概率分析去除历史数据的离群点。

3.1 基线算法:

说明一下，下文异常检测的场景，更多是实时检测最新一个点的数据(聚合后)是否异常。

环比

对于现实中绝大部分的异常或故障，最直观的表现就是突然的下跌(请求量，成功量)，所以根据数据环比生成基线，并检测异常是一种最简单也是最有效的策略.

1) 移动平均/加权移动平均/指数加权移动平均: 因为监控数据最大的一个特性就是有序，所以理论上当前时刻的点与越靠近它的点关联越大。指数加权移动平均(EWMA)就是这个特性的最佳实践，而且这个公式真的是太优雅了:

EWMA(1) = p(1)  // 有时也会取前若干值的平均值。α越小时EWMA(1)的取值越重要。

EWMA(i) = α * p(i) + (1-α) * EWMA(i – 1) //α是一个0-1间的小数，称为smoothing factor.
如果α = 0.2，l = [p(1)，p(2)，p(3)，p(4)]
EWMA(1) = p(1)EWMA(i) = 0.2 * p4 + 0.8 * (0.2*p3 + 0.8 * (0.2 * p3 + 0.8 * p4))= 0.2(p4 + 0.8*p3 + 0.8*0.8*p2 + 0.8*0.8*0.8*p1)= 0.2(p4 + 0.8^1*p3 + 0.8^2*p2 + 0.8^3*p1)
所以为什么叫做指数加权移动平均!! 而且系数α越大，越靠近当前时间的点，权重越大，曲线的平稳性越差.

(ps. 这个公式真的太优雅了)

但在应用的过程中也发现一定的缺点: 上升下降福度大的曲线，即使是指数加权移动平均拟合较差，会出现一定延迟: (暂时没有图，自己脑补一下吧)

根本原因是之前(moving average和EWMA)，我们假设相邻两个点的趋势(Δy/Δx)是一样的，但现实往往不是这样的，所以前人发明了一个东西叫做 Double EWMA，开始既考虑量(level)，也考虑趋势(trend). 公式还是一贯的简洁优雅:

但是.. 聪明的你一细想，数据都是具有周期性的，既然已经考虑了量(level)和趋势(trend)，是否可以把过去14天，每天这个点的周期数据(seasonal)也考虑进去呢?

这个东西叫做 Triple EWMA，其实就是大名鼎鼎的 Holt-Winters Method! 但这已经不仅仅是环比了，是环比+同比的综合决策，所以留个悬念，留到第三部分介绍。

2) 曲线拟合 - 多项式回归(polynomial regression): 最近在学吴恩达的机器学习课程，看到 linear regression 的时候，灵机一动，这不是完全为环比基线而生的。

具体不展开了，只能说效果还是挺不错的。

同比

很有趣的一个事实: 就算是小众业务的流量，每分钟一二十的请求量，每天的趋势和量级几乎是一致的: 24h的规律，白天上涨，晚上下跌。可以看下图，绿线表示今天的数据，红线表示过去七天的数据。

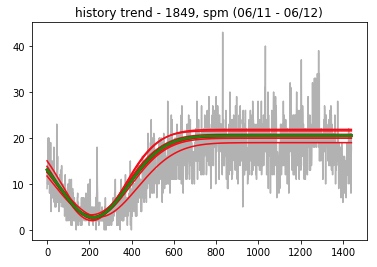
所以自创了一种同比算法: 当今日与历史趋势一致时(余弦相似性)，平移历史数据作为今日的基线。

环比 + 同比

外卖订单量预测异常报警模型实践 那篇文章给我的最大启发是异常检测可以将数据抽象为一个二维的矩阵，去检测右下角的那个点是否为异常:

上文提到的 Triple EWMA(Holt-Winters Method)，就是对这个抽象模型的最佳实践(level+trend+seasonal):

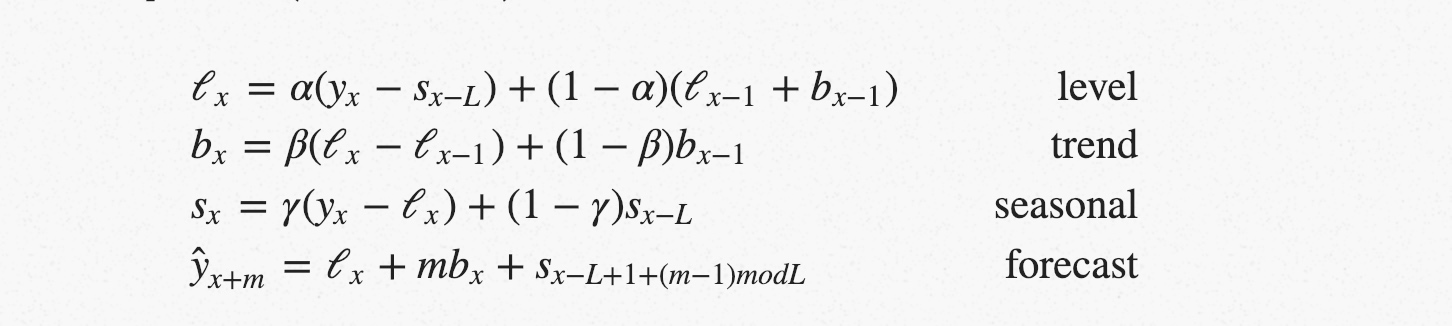
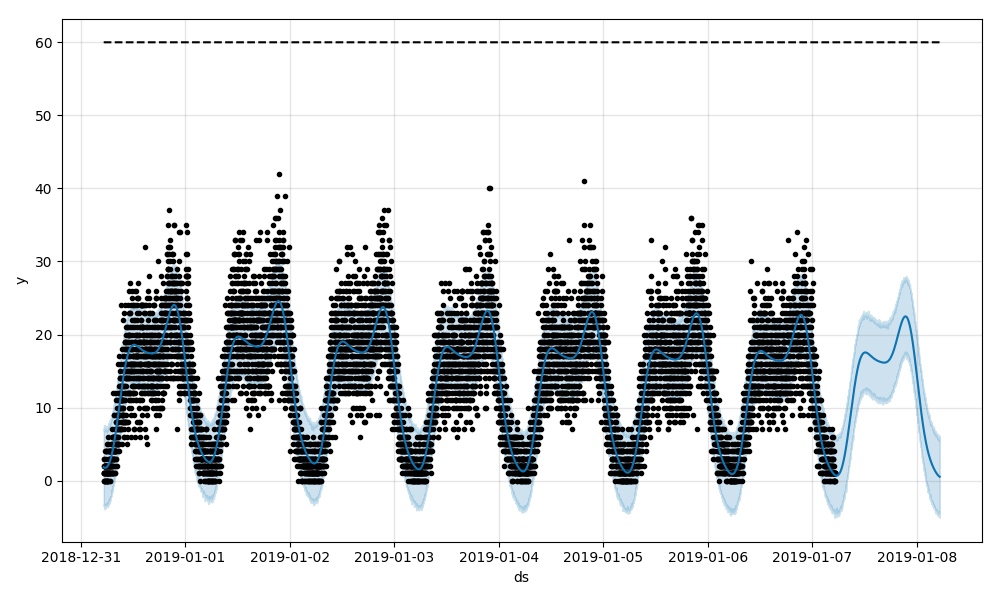
Facebook 开源了一个周期性异常检测的开源库，叫做 prophet，我实验了一下，还是挺友好的(下图为真实监控数据，一月八号为预测):

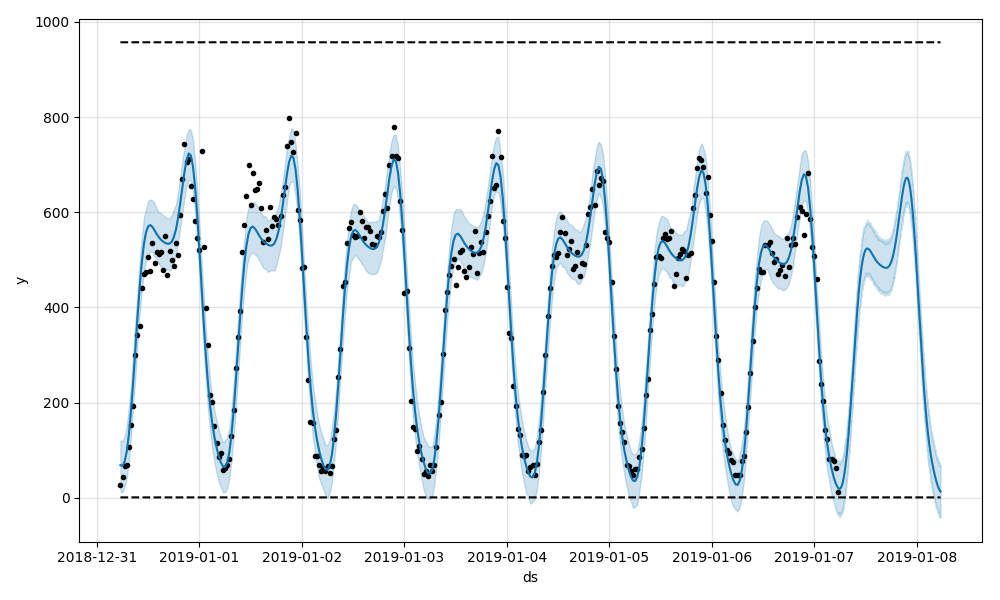
30 min 聚合后的效果:

prophet 实际的原理可以参考：https://zr9558.com/2018/11/30/timeseriespredictionfbprophet/

3.2 阈值算法

传统的静态阈值不太合理，例如当前分钟环比下跌超过 30% 认为异常，但在数据平缓的时候，可能 下跌 10%就是一个很明显的异常了：

  1. 静态阈值: 取监控系统配置上配置的阈值
  2. 动态阈值: 根据历史振幅区间(选取3-sigma去除异常点后的最大值和最小值)生成阈值

4. 汇总结果

不同的基线算法与阈值算法可以相互结合，生成结果。例如如果有四个基线算法，两个阈值算法，最终可以最多获得6个判断结果。然后采用投票者的模式: 只要大于或等于两个结果判断为噪音，就认为此报警为噪音。

5. 告警感知

  1. 告警的可视化：
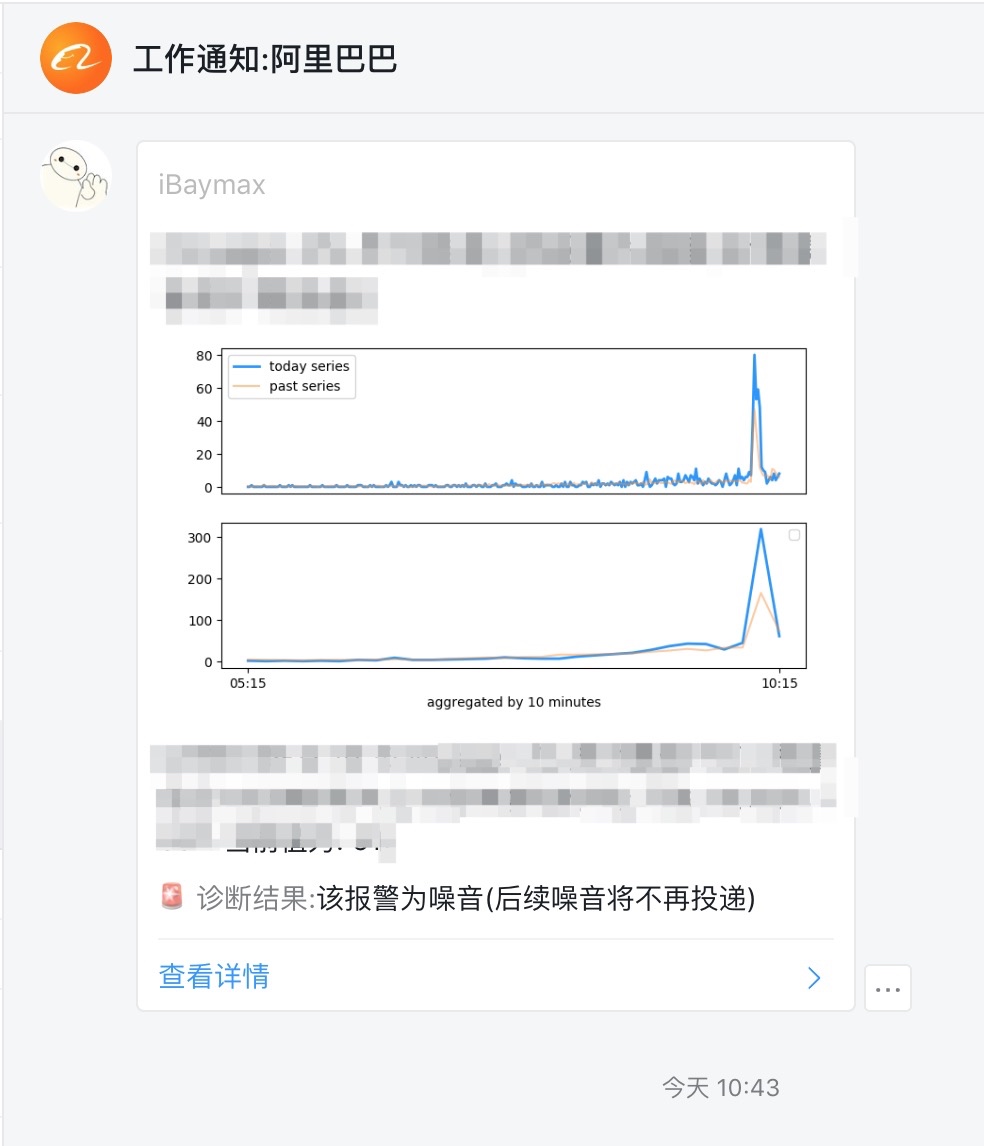
  2. 因为我个人很不希望降噪算法对用户来说是一个完全的黑盒，所以点击告警后，详情页会给出降噪的原因。

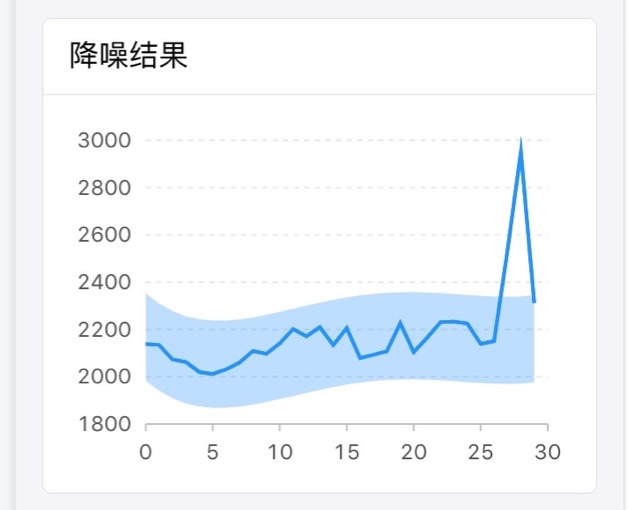
数据统计

  1. **千人千面的告警大盘：**快速暂时选择的时间段，一共收到了多少告警？其中多少是噪音(nonactionable)？哪个监控，业务线，或商户创造的最多的 toil?
  2. **告警列表页：**聚合连续的告警。

其他遗憾

  1. **更加丰富的输入：**对于文中的告警，输入仅仅为 30分钟 * 8天 的一个矩阵，但其实可以丰富其他各种特征作为输入。。但这里又有一个矛盾，更多特征意味着更加黑盒。或者说加上半监督的形式，因为假设这种情况两条一模一样的曲线，有的认为是故障，有个可能又是噪音。
  2. **投票的模式诟病：**虽然有人工标记测试集的回归，尽量让算法组合变得"敏感”。但有两个结果是噪音就认为该告警为噪音的策略还是有点不够 robust. 考虑是否可以改为如果有一定的异常就认为是真实故障，这样的好处是不断去覆盖异常检测的场景，而不是尽可能的去降噪。
  3. **降噪的不同形式：**在降噪实现的过程中，过于专注于对流量的分析。但实际上降噪的 scoop 可以更大，例如：
    • 合理的分派策略，例如设置自动的 oncall 排班处理告警，以及对应的升级策略(不断增大投递的范围)，参考 pagerduty
    • 同一时间的大量告警的横向聚合为事件投递
    • 长时间没人阅读或处理的告警，将会被降级
  4. 人对告警的忍受度太高了。。
  5. …

业内降噪产品：

欢迎补充

  1. onealert：现在改名叫做睿象云，这个域名。。。https://aiops.com/CAIntroduce.html
  2. pagerduty: https://www.pagerduty.com/
  3. …

Reference:

感谢这些让我受启发的好文章:

  1. https://grisha.org/blog/2016/01/29/triple-exponential-smoothing-forecasting/
  2. https://tech.meituan.com/2017/04/21/order-holtwinter.html
  3. http://facebook.github.io/prophet/
  4. …