数据库查询的索引原理介绍 (面试必问)
分享一个小故事: 依稀记得人生第一次面试终面的时候, 那家公司的CTO问我数据库中有哪些索引. 正好读书时学过一门课叫做DBMS Implementation, 于是就巴拉巴拉列了一堆. 瞬间面试官就两眼发光的看着我, 说我既然知道bitmap, 一定是个上课认真学习的好孩子, 就兴高采烈的给我发了offer.
所以说年轻人, 认真读了这篇博客之后, 你就可以顺利的拿到offer, 从此走上成为CTO赢取白富美的康庄大道!
p.s. 写的稍微有些粗糙, 有不明白的可以直接给我留言或发邮件, 笔芯.
目录:
- 一个属性的查询
- 线性扫描
- 二分查找
- Hashing
- B-Tree
- 多个属性的查询
- Bitmap!
- MA.Hashing
- Grid Files
- kd-Trees
- Quad Trees
一个属性的查询
通俗的说, 就是select语句后边, 只对一个属性进行过滤, 例如:
select * from Employees where id = 15567;
select * from Employees where age = 25;
select * from Employees where age>20 and age<50;
常用的算法如下:
线性扫描
因为如果b条记录是无序的, 只能通过线性扫描进行查找.
时间复杂度: 最好 O(1), 平均 b/2, 最差 b
题外话+1: 对于乱序存储, 每条记录(tuple)直接存在一个文件(heap file)中. 删除记录: 标记删除而不是物理删除. 添加记录: 在文件的最末端插入一条记录.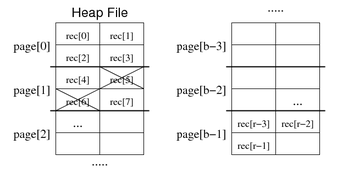
二分查找
如果记录是有序存储的话, 自然想到可以用二分查找.
这么做查询虽然起飞了, 但插入数据的效率降低了(每插入一个数据都要重新更新保存所有数据. 这个世界就是这样, 无论什么都是有trade off的).
所以对数据库的有序存储做了一个优化: 首先按范围分好区间, 每一块代表一个page(见下图), 当某个区间存满了之后, 会链接(link)一个新的Overflow Page继续存储. 因为大部分情况下, 都是少量的插入与删除(Large-scale file re-arrangement occurs less frequently). 最终可以二分查找搜索page, 再去遍历搜索具体的记录.
时间复杂度: 最好 O(1), 最差 Ov * (log2b + bov) (Ov代表每个page记录的大小, bov代表Overflow Page的数量)
题外话+1: 想起之前面试的一道题: 二分查找搜索范围
Hashing
最简单就是取余. 例如有数组[1, 3, 4, 7, 8, 9], 并假设只有3个page可以存储, 就对每个数字除以3取余: [1, 0, 1, 1, 2, 0], 其中每个数字就对应插入和查询的位置(page0, page1, page2).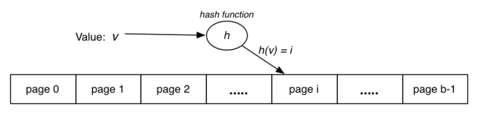
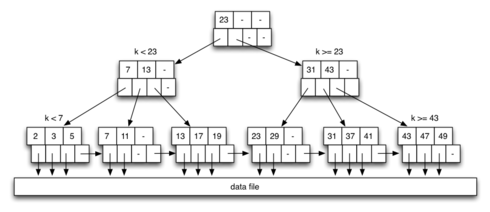
B-Trees
太经典了, 就不多说了. 参考我的另一篇博客: <算法导论(3rd)>第十八章 - B Tree!
其他
例如保存一个page的最大值和最小值, 如果不满足搜索条件就直接跳过.
还有就是类似倒排索引的形式利用空间换时间.
多个属性的查询
Bitmap!
不多解释了, 看图. 所以查询颜色为red, 并且小于$4的所有记录, 只需要对100011和110001做与操作就可以了, 太酷了.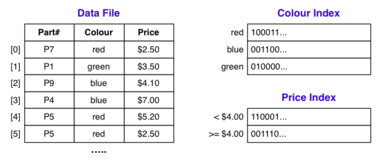
MA.Hashing(Multi-attribute Hashing)
取多个字段hash值的最后一位, 组成一个新的hash. 唯一的缺点是, 不像单个字段的hash, 永远返回的是一个page, MA.Hashing会返回多个pages.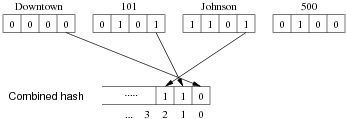
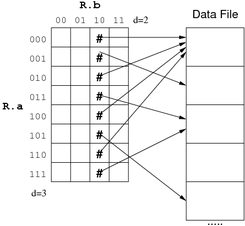
Grid Files
将数据按属性 a 和 b 分成4*8的表格, 所以:
select...where a=C1 and b=C2: 查询一个单元格 对应的数据.select...where a=C1: 查询一行(四个单元格)select...where b=C2: 查询一列(八个单元格)
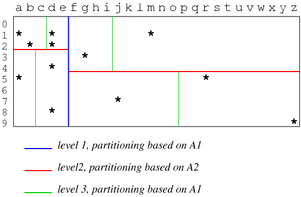
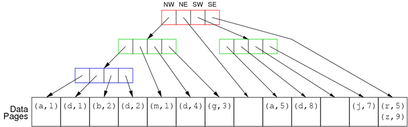
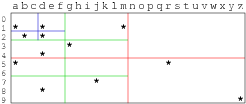
kd-Trees
将下边的两张图联系起来看就明白了, 实际上就是对一个二维空间按条件做了划分. 查询时也能按条件快速查找.
Quad Trees
和kd-Trees其实大同小异, 看下图你就明白了:
轻松一下
厉害竟然读到最后了, 给你开心一下, 分享老师的一些有趣回复: