..
<算法导论(3rd)>第十八章 - B Tree!
之前学DBMS的时候接触到B Tree, 但当时懵懵懂懂我的对B Tree的操作也是一知半解.
今天看了书(主要是严谨的定义和完整的伪代码流程), 感触颇深, 以此博客记录一下.
B Tree的定义:
(看上去这些定义好像很啰嗦没什么意思, 但花点时间搞清楚后, 看伪代码和下文会清晰很多.)
- 每个节点x有以下的性质
x.n→ 一个节点中关键字的个数.x.key1 <= x.key2 <= x.key3, e.g. 一个节点: [A, N, O] → A < N < Ox.leaf→ 是否为叶子节点(True/False)
- 每个节点如果有n个关键字, 就有n+1个指向孩子的指针**(x.c1, x.c2, …)**
- 每个叶子节点, 都有相同的深度, 即树的高度h (为什么呢? 每个叶子节点…)
- 对于两个相邻关键字x.key1, x.key2之间(子树上)的任意一个关键字k, 必定有x.key1 <= k <= x.key2
- 最后有个很重要的概念: 最小度数(minimum degree) → t.
得到一个节点关键字个数限制: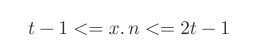
B Tree的优势:
B Tree最大的优势: 相对较小的磁盘存取次数.
为什么呢? 因为大部分的操作的时间复杂是和B Tree的高度成正比的(每次查询一个节点都需要一次磁盘访问, 例如查询一个叶子节点需要访问h(高度)个节点).
B Tree的高度(具体证明见书, 其实也是等比数列的求和):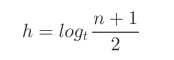
而二叉树的高度: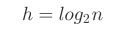
可以看到B Tree的高度的对数的底可以比2大很多倍, 所以总高度会比二叉树小很多, 从而避免了大量的磁盘访问:
B Tree的搜索:
直观的说就是:
- 遍历节点中的所有关键字, 选择分支 → 找到子节点 | 输出None(x.leaf==True).
- 对子节点递归做第一步操作.
B Tree的插入 (敲重点):
- B-TREE-INSERT(T, k)
- 伪代码:

第2-8行: 其实就是对root节点为full的情况(x.n >= 2t+1)做了一个特殊处理, 进行split操作.
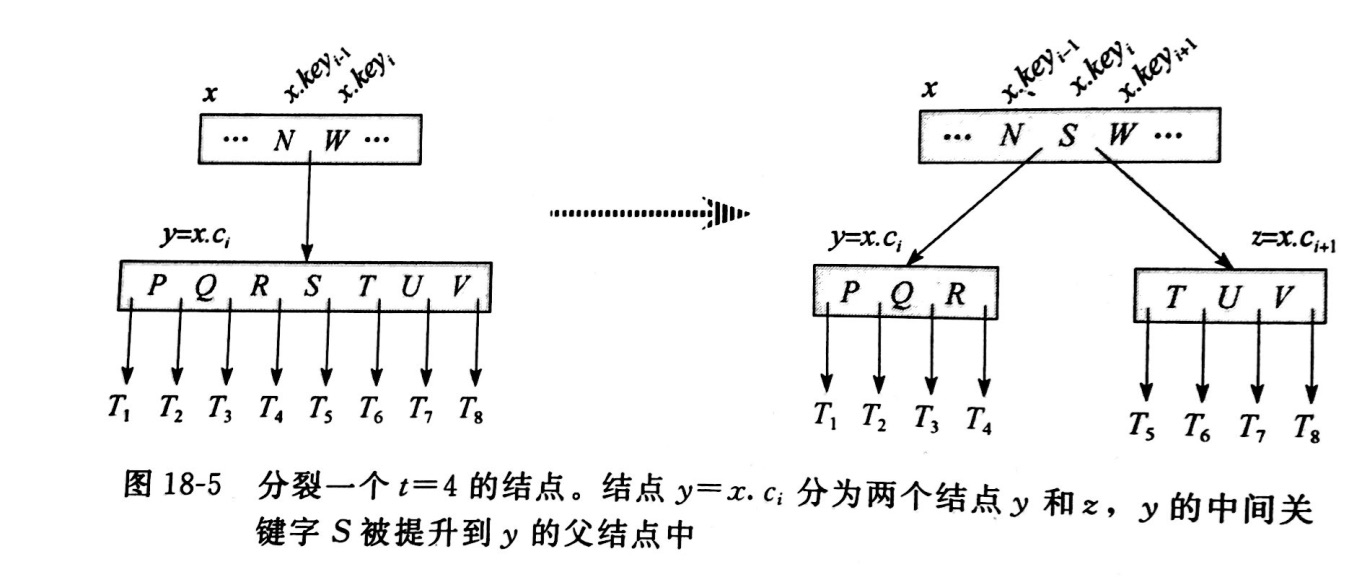
第8行: SPLIT操作图解: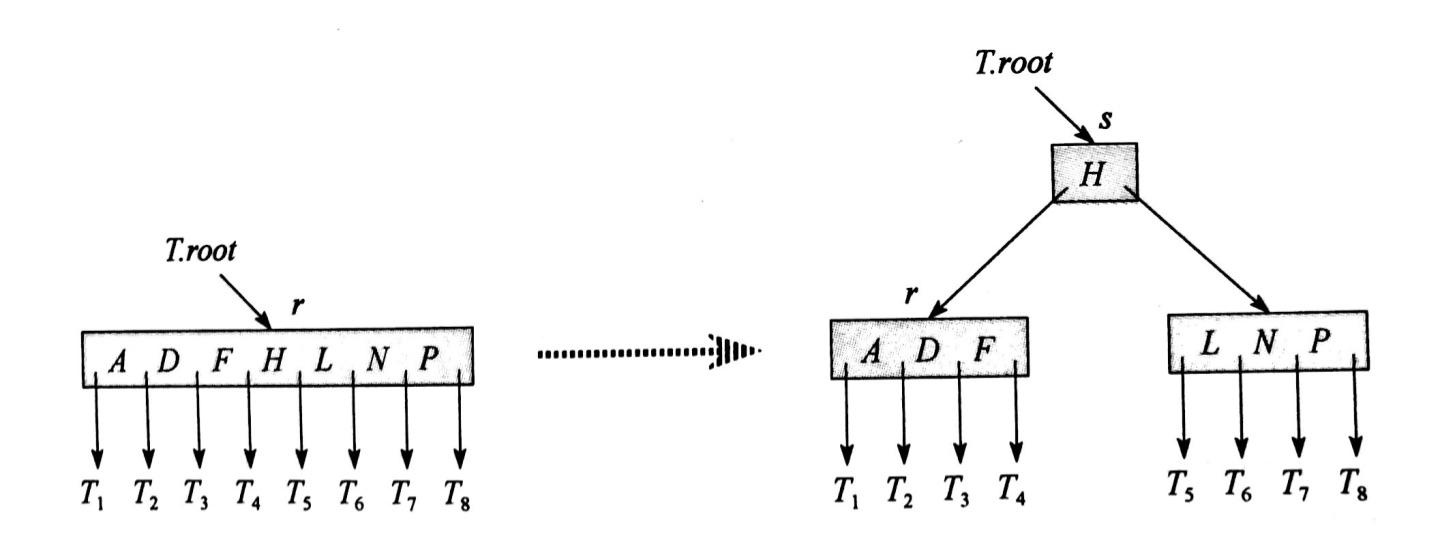
- 伪代码:
- 调用子方法 B-TREE-INSERT-NONFULL:

上图的分析:- 如果是叶子节点(x.leaf==True):
就遍历节点中的关键字, 找到正确的位置插入. - 否则:
- (1) 遍历节点中的关键字, 找到正确的位置(指针)
- (2) 判断该指针指向的子节点是否为full
- (3) 如果是就对这个子节点做分割(split).
- (4) 递归调用B-TREE-INSERT-NONFULL
- 如果是叶子节点(x.leaf==True):
B Tree的删除:
(TODO)