Henry Z's blog
<算法导论(3rd)>第六章 - Heap!Heap!Heap!
第一次懵懵懂懂接触Heap是在学信息检索的时候, 讲到用min heap直接在disk上对posting lists做合并操作.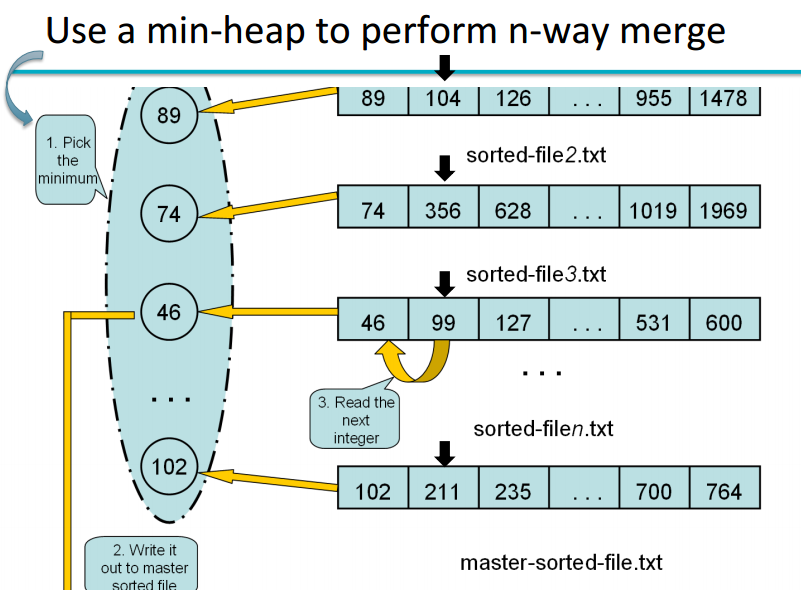
今天看了<算法导论(3rd)>第六章堆排序, 感触颇深, 以此博客记录一下.
6.1 堆:
概要
(二叉)堆可以看作为一个完全二叉树. 个人觉得它最神奇的特性就是每个相邻节点(父节点/左孩子/右孩子)的关联关系可以轻松取到:
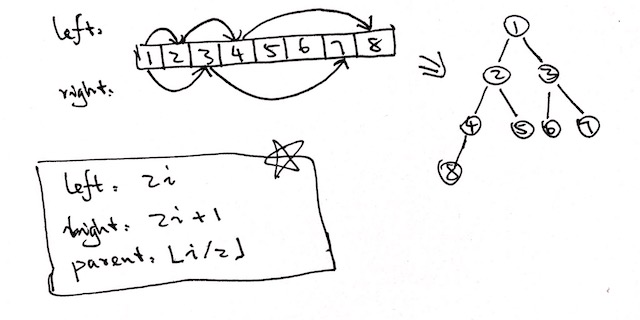
二叉堆又分为最小堆和最大堆.
定义: 对于每个节点(除了root节点), 左孩子和右孩子的值都小于父节点(左右孩子的值并没有顺序).
练习:
(TODO)
6.2 维护堆的性质:
MAX-HEAPIFY:
发现看了一会文字描述, 云里雾里的, 还不如直接看伪代码, 瞬间就明白了:
大意就是说, 在一个最大堆中, 选取一个node(A[i]), 如果max(node.val, node.left.val, node.right.val)是node.val, 程序结束; 否则就将node和left和right中的较大的交换. 交换之后, 递归调用MAX-HEAPIFY(A, i)
练习:
(TODO)
6.3 建堆:
BUILD-MAX-HEAP:
SHOW ME THE CODE: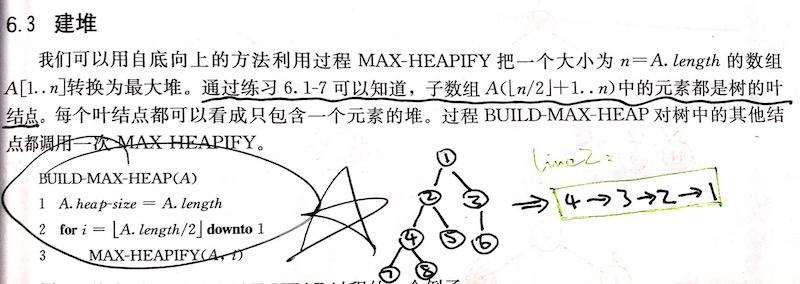
伪代码的第二行可能有些看不懂, 意思就是说对所有非叶子节点, 从右到左, 从下到上, 循环执行上一章的MAX-HEAPIFY(6.3-2: 对循环执行顺序的解释.)
练习:
(TODO)
6.4 堆排序算法:
HEAPSORT = BUILD-MAX-HEAP(6.3) + MAX-HEAPIFY(6.2):
伪代码:
上图中每个循环的核心思想就是:
- 将第一个元素(当前堆的最大值)和最后一个元素交换
(line 3) - 取出当前最大值, 并对之前的最后一个元素(交换后为第一个元素, A[1])做MAX-HEAPIFY(A, 1)
(line 5)
练习:
(TODO)
6.5 优先队列(priority queue):
一个最大优先队列支持以下四个操作:
1) MAXIMUM:
返回S中具有最大值的元素(就是返回第一个元素) → return A[1]
2) HEAP-EXTRA-MAX:
和MAXIMUM不同的是, 除了获取到最大元素, 还要将此元素从优先队列中取出.
伪代码:
其实就是6.4 堆排序中的第一次循环.
3) HEAP-INCREASE-KEY:
意思就是说将某个元素A[i]更新值(变大), e.g. 3 → 13…
伪代码:
说明:
如果大于parent.val就一直和parent做交换.
4) MAX-HEAP-INSERT:
这个就比较神奇了, 插入一个新元素, 但强行使用HEAP-INCREASE-KEY来实现:
个人思考:
堆排序是否也可以使用 MAX-HEAP-INSERT + HEAP-EXTRA-MAX实现呢? 时间复杂度也是O(lg n)
练习:
(TODO)
思考题:
TODO